题目

the leetcode link

搜索旋转排序数组
整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

示例 1：
输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4
示例 2：
输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1
示例 3：
输入：nums = [1], target = 0
输出：-1

提示：
1 <= nums.length <= 5000
-10^4 <= nums[i] <= 10^4
nums 中的每个值都 独一无二
题目数据保证 nums 在预先未知的某个下标上进行了旋转
-10^4 <= target <= 10^4

进阶：你可以设计一个时间复杂度为 O(log n) 的解决方案吗？

思路

二分查找法

Q:翻转数组的样子是怎么样的？
A:部分有序。
Q:划分中值后，有什么规律？
A:一定有一侧是有序的。
Q:有序侧和无序侧对查找有何影响？
A:有序侧能通过between比较方式，O(1)时间判断target是否存在；
无序侧仅靠自身不能以O(1)时间判断存在，要借助有序侧判断。
因此，我们先判断哪一侧是有序侧，再通过between比较方式判断target在不在有序侧，不在有序侧则说明是在无序侧，不断缩小范围，反复判断。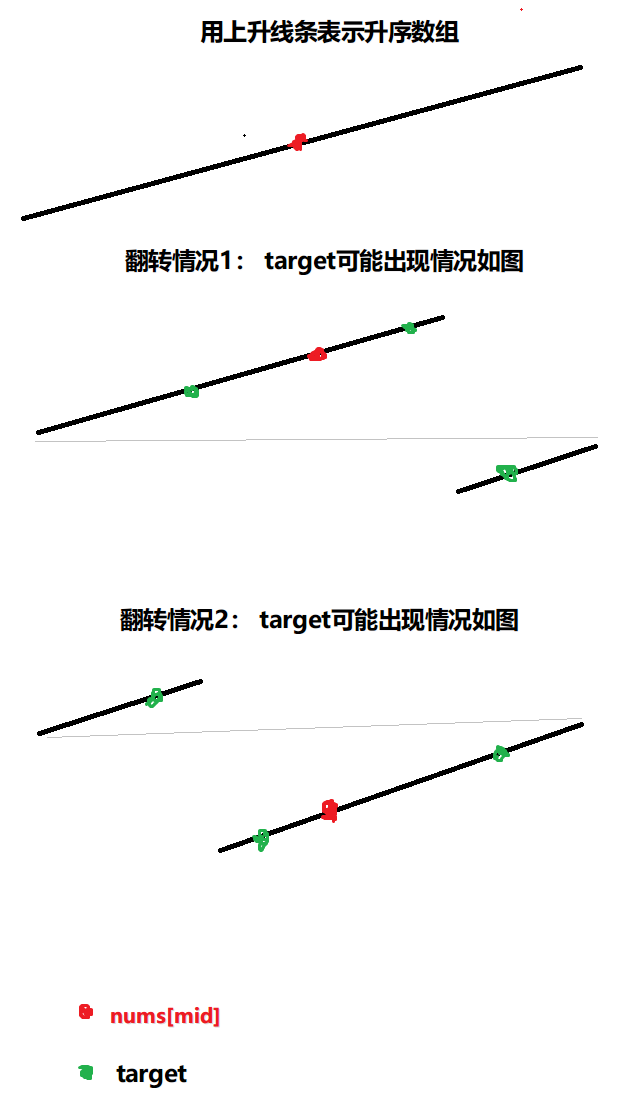

binary.png

binary.png

left 最左下标；right 最右下标；mid中间值下标；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
翻转情况1：
条件：nums[left]<=nums[mid]
    图中target可能出现情况依次是：
    1. nums[left]<= target <= nums[mid]     （左侧绿点，有序侧）
    2. target >= nums[mid]                  （右侧1绿点）
    3. target <= nums[left]                 （右侧2绿点）
2,3合并为 !(nums[left]<= target <= nums[mid])


翻转情况2：
条件：nums[left]> nums[mid]
    图中target可能出现情况依次是：
    4. target >= nums[right]                （左侧1绿点）
    5. target <= nums[mid]                  （左侧2绿点）
    6. nums[mid]<= target <= nums[right]    （右侧绿点，有序侧）
4,5合并为 !(nums[mid]<= target <= nums[right])

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
    public int search(int[] nums, int target) {
        int n = nums.length;
        int l = 0;
        int r =n-1;
        while(l<=r){
            int m =(l+r)>>>1;
            if(nums[m] == target){ //中值等于马上返回
                return m;
            }

            if(nums[l]<=nums[m]){       //翻转情况1

                if(nums[l]==target){ //左值等于马上返回
                    return l;
                }else
                if(nums[l]<target && target<nums[m]){
                    r=m-1; //target情况1
                }else{
                    l=m+1; //target情况2,3
                }
            }else{                      //翻转情况2

                if(nums[r]==target){ //右值等于马上返回
                    return r;
                }else
                if(nums[m]<target && target<nums[r]){
                    l=m+1; //target情况6
                }else{
                    r=m-1; //target情况4,5
                }
            }
        }
        return -1;
    }
}